Презентация на тему виды симметрии

симметрия растений

У растений встречаются следующие виды симметрии:

• сферическая — симметричность при вращении в трёхмерном пространстве на произвольные углы;
• радиально-лучевая — симметричность при повороте вокруг какой-либо оси (много плоскостей симметрии, которые пересекаются в центре);
• двусторонняя (билатеральная) симметрия — симметричность относительно плоскости;
• трансляционная симметрия — симметричность при сдвиге в каком-либо направлении на некоторое расстояние.

Самыми распространенными видами симметрии являются билатеральная и радиально-лучевая.

Именно на билатеральную (зеркальную) симметрию листьев и радиальную симметрию цветов мы и обратили внимание осенью, играя в школьном саду. Эти два вида симметрии с необычным упорством повторяются вокруг нас

Особенности внешней формы часто находятся в прямой зависимости от особенностей внешнего воздействия. Господство симметрии в природе объясняется силой тяготения, действующей во всей Вселенной.

Все то, что растет по вертикали, то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой симметрии в виде веера пересекающихся плоскостей симметрии.

Все то, что растет горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии (одна плоскость симметрии). В самом деле, цветочные чашечки, обращенные кверху (ромашка, подсолнечник), имеют, как мы уже знаем, целый веер пересекающихся плоскостей симметрии. В то же время листья и цветы, расположенные на стебле сбоку (душистый горошек, орхидея и др.), обладают только одной плоскостью симметрии.

Симметрией обладают не только листья и цветы растений, но и их плоды и семена.

Диссимметрия и асимметрия

Если смотреть на природу строгим взглядом математика, то можно отметить отсутствие идеальной симметрии. Это обусловлено процессом постоянного роста и деления клеток, а также влиянием факторов внешнего окружения. К примеру, основу живых организмов составляют киральные биомолекулы, чьи компоненты не обладают симметрией между своими правыми и левыми сторонами.

Диссимметрия является частичной несоразмерностью отдельных элементов композиции. Для диссимметрии характерно произвольное расположение частей в рамках симметричной системы.

Полное нарушение принципов симметрии обуславливается понятием «асимметрия», что в переводе с древнегреческого языка означает — «несоразмерность». С древнейших времен асимметричные элементы использовались в искусстве, а также в зодчестве. Особенность приема заключается в создании единого гармоничного образа, состоящего из разнородных частей, пребывающих в визуальном равновесии.

В традиционной архитектуре по принципам асимметрии были возведены средневековые замки Европы:

• Замок Гродно в Нижней Силезии.
• Вентспилский замок в Латвии.
• Замок герцогов Бретонских во Франции.

Ярким образцом архитектурной асимметрии можно назвать Храм Василия Блаженого в Москве.

Краткий период постмодерна обогатил архитектуру многообразием асимметричных форм. Вот примеры некоторых из них:

• Музей Гуггенхайма в Бильбао.
• Бизнес-центр «Доминион Тауэр» в Москве.
• Центральная библиотека в Сиэтле.

Слайд 14 Поворотная симметрия.Предположим, что объект совмещается сам с собой

(или кратный этой величине),     где n = 2, 3, 4,

… В этом случае говорят о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка. Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180° вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой. Иными словами, буква «И» симметрична относительно поворота на 180°. Заметим, что поворотной симметрией обладает также буква «Ф».

На рисунке даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го.

Симметрия человека

Тело человека, как и тела многих живых существ, обладает билатеральной симметрией, которая проявляется в дублировании жизненно важных органов (легкие, почки, конечности, глаза, слуховые анализаторы и др.).

Но симметрия выражена не с абсолютной точностью, при этом степень отклонения от симметрии может демонстрировать уровень адаптированности к конкретным видам деятельности.

Внешне человек построен симметрично: левой руке всегда соответствует правая, и обе руки совершенно одинаковы!

НО! Если бы наши руки и в самом деле были совершенно одинаковы, то левая перчатка подходила бы и к правой руке, но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале.

Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела и старались подчеркнуть это в своих произведениях. Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи

Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя)

Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя).

Физическая симметрия тела и мозга не означает, что правая сторона и левая равноценны во всех отношениях

Достаточно обратить внимание на действия наших рук, чтобы увидеть начальные признаки функциональной асимметрии. Лишь немногие люди одинаково владеют обеими руками, большинство же имеет ведущую руку, чаще всего правую

Но, во всяком случае, внешне все люди симметричны. Известно, что люди считают лица, обладающие симметрией, более красивыми. И фигура человека считается красивой, если она соответствует законам симметрии и пропорциональна. Напротив, если симметрия тела нарушается, это не только внешне выглядит некрасиво, но и может стать причиной заболевания. Например, сколиоз (искривление позвоночника) – нарушение осанки может стать причиной заболеваний внутренних органов.

И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния.

Но полная безукоризненная симметрия выглядела бы нестерпимо скучно. Именно небольшие отклонения от неё и придают характерные, индивидуальные черты. На фоне общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например, расчесывая волосы на косой пробор — слева или справа или делая асимметричную стрижку.

Или, скажем, помещая на костюме асимметричный кармашек на груди. Лишь на одной стороне груди носятся ордена и значки (чаще на левой).

Порой человек старается подчеркнуть, усилить различие между левым и правым. В средние века мужчины одно время щеголяли в панталонах со штанинами разных цветов (например, одной красной, а другой черной или полосатой). В не столь отдалённые дни были популярны джинсы с яркими заплатами или цветными разводами. Но подобная мода всегда недолговечна. Лишь небольшие, тактичные отклонения от симметрии остаются на долгие времена.

Слайд 4 Осевая (зеркальная) симметрия.Фигура называется симметричной относительно прямой а,

прямой а также принадлежит этой фигуре. Прямая а называется осью

симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.На рисунке показан простой пример объекта и его зазеркального двойника – треугольник ABC и треугольник А1В1С1 (здесь MN – пересечение плоскости зеркала с плоскостью рисунка). Каждой точке объекта соответствует определённая точка зазеркального двойника. Эти точки находятся на одном перпендикуляре к прямой MN, по разные стороны и на одинаковом расстоянии от неё. Объект на рисунке выбран для простоты двухмерным. В общем случае объект (и соответственно его зазеркальный двойник) является трёхмерным. 

Осевая соразмерность

Осевая симметрия в архитектуре применялась в проектах культовых и дворцовых ансамблей, организации квартальной застройки городов, планировании парковых комплексов. При этом взаимное симметричное размещение архитектурных объемов соподчинялось срединной оси композиции, проходящей в виде прямой линии по центральной части главных улиц, транспортных магистралей и парадных аллей, которые могли служить путями продвижения торжественных процессий.

Можно сказать, что этот прием является характерным для объектов, расположенных на горизонтальной плоскости и занимающих значительные площади.

В качестве примеров следует отметить:

• Запретный город в центре Пекина.
• Центральная часть Санкт-Петербурга.
• Парковый комплекс в Версале.

СИММЕТРИЯ В ХИМИИ

Симметрия обнаруживается также и на атомном
уровне изучения вещества. Она проявляется в недоступных непосредственному
наблюдению геометрически упорядоченных атомных структурах молекул.

В 1810 году Джон Дальтон, желая показать
своим слушателям как атомы, комбинируясь, образуют химические соединения,
построил деревянные модели шаров и стержней. Эти модели оказались превосходным
наглядным пособием.

Молекула воды имеет плоскость симметрии
(прямая вертикальная линия). Ничто не изменится, если поменять местами парные
атомы в молекуле; такой обмен эквивалентен операции зеркального отражения

Исключительно важную роль в мире живой
природы играют молекулы ДНК (дезоксирибонуклеиновая кислота). Это двуцепочечный
высокомолекулярный полимер, мономером которого являются нуклеотиды. Молекулы
ДНК имеют структуру двойной спирали, построенной по принципу комплементарности.

Прием отражения в архитектуре

Зеркальная симметрия — это наиболее распространенный прием, используемый в традиционной архитектуре. Суть его заключается в зеркальном копировании одной части здания относительно другой посредством центральной плоскости симметрии, вырождающейся в вертикальную прямую, проходящую обычно через центральный вход. Этот вид симметрии главным образом использовался при решении фасадов сооружений, подчеркивая их значимость.

Гармония в природе и человеческом обществе была основной темой, которую олицетворяла собой зеркальная симметрия. Большая часть храмов и дворцов древних цивилизаций Египта, Месопотамии, античных Греции и Рима построена по этому принципу, что можно увидеть в архитектурной композиции сохранившихся зданий, а также на картинках, воссоздающих внешний облик безвозвратно утраченных. Среди них можно выделить:

• Храм богини Изиды на острове Филе.
• Ворота Иштар.
• Древнегреческий храм Парфенон на афинском Акрополе.
• Древнеримский храм Портуна на Бычьем форуме в Риме.

В I тысячелетии нашей эры были возведены величественные культовые сооружения в Южной Европе, Индии, Китае, Мезоамерике, где в композиции фасадов использовалась зеркальная симметрия:

• Собор Святой Софии в Константинополе.
• Индуистский храм Ранганатхи в Шрирангаме.
• Дачаньдянь — Дворец Великих Свершений в Китае.
• Храм Воинов в Чичен-Ице.

В средневековой архитектуре Европы, Ближнего Востока, Средней Азии, Японии также применялся принцип зеркальной симметрии:

• Пизанский собор.
• Миланский собор.
• Собор Парижской Богоматери.
• Мечеть Масджид аль-Харам — Заповедная мечеть в Мекке.
• Мечеть Калян в Бухаре.
• Храм Феникса монастыря Бёдо-ин в Японии.

Эпоха Ренессанса, возродившая античные культурные традиции, оказала значимое влияние на развитие архитектуры эпох Просвещения и Нового времени. Здания этих исторических периодов построены с неизменным соблюдением общего правила зеркальной симметрии:

• Собор Святого Петра (Рим).
• Церковь Санта-Сусанна (Рим).
• Собор Святого Павла (Лондон).
• Исаакиевский кафедральный собор (Санкт-Петербург).

Слайд 92.Симетрия в живой природе 2.1. Понятие симметрии. Слово «симметрия» имеет двойственное толкование.В

одном смысле симметричное означает нечто пропорциональное, сбалансированное; симметрия показывает тот способ согласования многих частей, с помощью которого они объединяются в целое. Второй смысл этого слова — равновесие.Симметрия(в широком смысле) — свойство геометрической фигуры, характеризующее некоторую правильность формы данной фигуры, неизменность её при действии движений и отражений.Симметрия(с греч.) — соразмерность, равно, подобие, равномерие, соответствие, сходность; одинаковость, либо соразмерное подобие расположенья частей целого, двух половин; сообразие, сообразность; противоравенство, противоподобие.Асимметрия(греч. asymmetria несоразмерность) в биологии — неупорядоченное расположение сходных (парных).

1.5. Зеркально-поворотная симметрия

Вырежем из плотной бумаги квадрат и впишем внутрь его косо другой квадрат (Рисунок 2.10).

Затем отогнем углы бумаги по линиям, ограничивающим внутренний квадрат (соседние углы отгибаются в противоположные стороны). В результате получим объект, показанный на рисунке 2.11.

Он имеет поворотную ось 2-го порядка (ось АВ) и не имеет плоскостей симметрии. Будем рассматривать изделия сначала сверху, а затем снизу (с противоположной стороны листа бумаги). Мы обнаружим, что никакого различия между «верхом» и «низом» нет; в обоих случаях объект выглядит одинаково.

В связи с этим возникает мысль, что поворотная симметрия 2-го порядка не исчерпывает всей симметрии данного объекта. Дополнительная симметрия, которой обладает наш объект, — это так называемая зеркально-поворотная симметрия: объект совмещается сам с собой в результате поворота на 90° вокруг оси АВ и последующего отражения в плоскости CDEF. Ось АВ называют зеркально-поворотной осью 4-го порядка.

Таким образом, здесь наблюдается симметрия относительно двух последовательно выполняемых операций – поворота на 90 и отражения в плоскости, перпендикулярной к оси поворота. Такой вид симметрии получил название зеркально-поворотной.

Слайд 8С симметрией мы встречаемся везде – в природе, технике, искусстве, науке.

Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. В своем проекте мы показали, что законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.

Мы узнали, что существует множество видов симметрии как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира. В нашей исследовательской работе отмечено так же, что помимо симметрии существует понятие асимметрии. Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте.

Слайды и текст этой презентации

Слайд 1ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА С УГЛУБЛЕННЫМ ИЗУЧЕНИЕМ ФРАНЦУЗСКОГО

ЯЗЫКА № 1244 САО ГОРОДА МОСКВЫПРОЕКТНАЯ РАБОТАБанников Григорий, Косарев Алексей

(7 класс «А»)Бритковская Александра, Руденко Анна (7 класс «Б»)«СИММЕТРИЯ В ЖИВОЙ ПРИРОДЕ»

Слайд 2ПАСПОРТ ПРОЕКТНОЙ РАБОТЫ
Цель проекта: изучить научно-популярную литературу и исследовать проявление

содержащуюся в печатных изданиях по этой теме.Рассмотреть какие виды симметрии встречаются в животном и растительном мире.Показать взаимосвязь видов симметрии в живой природе.Выявить межпредметные связи между учебными предметами: геометрией и биологией.Сделать выводы.Объект исследования: симметрия в растительном и животном мире.Предмет исследования: исследование особенностей различных типов симметрии в растительном и животном мире.Учебный год: 2011 — 2012.Руководители проекта: Орлова Наталия Александровна (учитель биологии);Красовская Наталья Петровна (учитель математики).

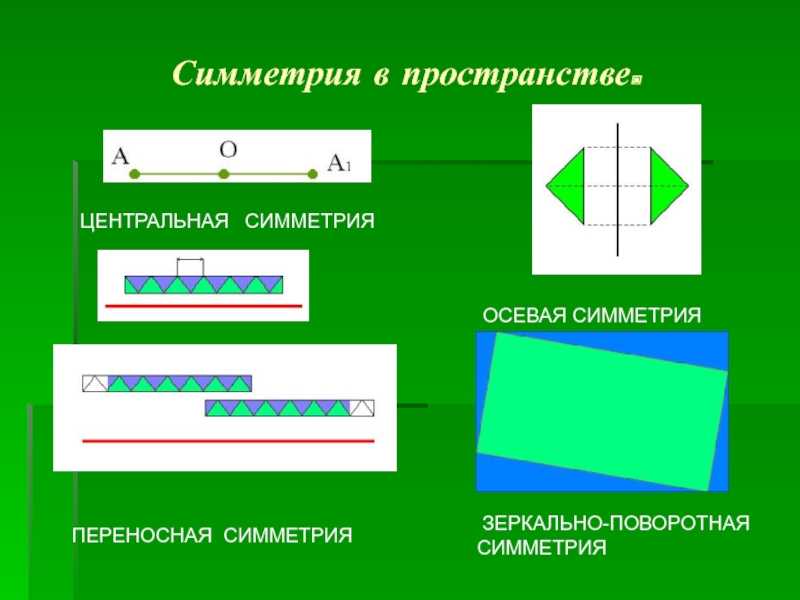
Слайд 3Симметрия в пространстве. ОСЕВАЯ СИММЕТРИЯ ЦЕНТРАЛЬНАЯ

СИММЕТРИЯ ЗЕРКАЛЬНО-ПОВОРОТНАЯ СИММЕТРИЯ ПЕРЕНОСНАЯ СИММЕТРИЯ

Слайд 4Исследование некоторых растений и животных на предмет выявления симметрии
Симметрия

в мире растений.Цветок капусты. Центральная (лучевая) симметрия и поворотная симметрия

4 порядка (угол поворота 90º).

Цветок гороха посевного – пример двусторонней (зеркальной) симметрии у растений.

Цветок вишни. Центральная (лучевая) симметрия и поворотная 5 порядка (угол поворота 72º).

Слайд 5Симметрия в мире растений.Мутовчатое расположение листьев на стебле (хвощ) –

расположение листьев на стебле Гибискуса китайского – пример винтовой симметрии у растений

Слайд 6Симметрия в мире растений.Шишки хвойных растений и лист рябины –

пример переносной симметрии у растений. Листья растений: монстеры привлекательной, клена,

дуба, орешника и березы – примеры двусторонней (зеркальной) симметрии у растений.

Слайд 7Симметрия в жизни животных.Морская звезда и панцирь морского ежа –

человека и мухи.

Асимметрия – амеба протей.

раковины брюхоногого моллюска Рапана.Соты осы – конструкторский шедевр, состоящий из

ряда шестигранных ячеек. Переносная симметрия.

мир многообразен и неповторим.В живой природе огромное большинство живых организмов обнаруживает сочетание различных видов симметрии.Симметрия позволяет живым организмам лучше приспособиться к среде обитания и просто выжить, причем у неподвижных и малоподвижных организмов распространена лучевая (радиальная) симметрия или симметрия относительно точки, а у активно передвигающихся организмов – двусторонняя (зеркальная) симметрия.Помимо симметрии в живой природе на микроуровне встречается и асимметрия.Проектная работа расширила наш кругозор и помогла взглянуть на окружающий мир глазами исследователя.Мы на практике увидели межпредметные связи между математикой и биологией, повысился интерес к изучению этих предметов в школе.Мы решили продолжить эту тему в следующем году, включив в исследования и тела неживой природы.Так, что исследование продолжается!

СИММЕТРИЯ В МАТЕМАТИКЕ.

Идея симметрии часто является отправным
пунктом в гипотезах и теориях учёных прошлых веков, веривших в математическую
гармонию мироздания и видевших в этой гармонии проявление божественного начала.
Древние греки считали, что Вселенная симметрична просто потому, что симметрия
прекрасна. В своих размышлениях над картиной
мироздания человек с давних времен активно использовал идею симметрии.

Древние греки полагали, что Вселенная
симметрична просто потому, что симметрия прекрасна. Исходя из соображений
симметрии, они высказали ряд догадок.

Так, Пифагор (5 век до н.э.), считая сферу
наиболее симметричной и совершенной формой, делал вывод о сферичности Земли и о
ее движении по сфере. При этом он полагал, что Земля движется по сфере некоего
«центрального огня». Вокруг того же «огня», согласно Пифагору, должны были
обращаться известные в те времена шесть планет, а также Луна, Солнце, звезды.

Широко используя идею симметрии, ученые
любили обращаться не только к сферической форме, но также к правильным выпуклым
многогранникам. Еще во времена древних греков был установлен поразительный факт
– существует всего пять правильных выпуклых многогранников разной формы. Симметрии
геометрических тел большое значение придавали греческие мыслители эпохи
Пифагора. Они считали, что для того, чтобы тело было «совершенно
симметричным», оно должно иметь равное число граней, встречающихся в
углах, и эти грани должны быть правильными многоугольниками, то есть фигурами с
равными сторонами и углами. Впервые исследованные пифагорейцами, эти пять
правильных многогранников были впоследствии подробно описаны Платоном.
Древнегреческий философ Платон придавал особое значение правильным
многогранникам, считая их олицетворением четырёх природных стихий:
огонь-тетраэдр (вершина всегда обращена вверх), земля-куб (наиболее устойчивое
тело), воздух-октаэдр, вода-икосаэдр (наиболее «катучее» тело).
Додекаэдр представлялся как образ всей Вселенной. Именно поэтому правильные
многогранники называются также телами Платона.

Простейшими видами пространственной
симметрии являются центральная, осевая, зеркально- поворотная и симметрия
переноса.

Центральная симметрия.

Две точки А и А₁
называются симметричными относительно точки О, если О – середина отрезка АА₁.
Точка О считается симметричной самой себе.

Осевая симметрия.

Преобразование
фигуры F в фигуру F₁, при котором каждая ее точка переходит в точку,
симметричную относительно данной прямой, называется преобразованием симметрии
относительно прямой а. Прямая а называется осью симметрии.

Если во внутрь
квадрата вписать с поворотом другой квадрат, то это и будет пример
зеркально-поворотной симметрии.

Переносная симметрия.

Если при переносе
плоской фигуры F вдоль заданной прямой АВ на расстояние а (или кратное этой
величине) фигура совмещается сама с собой, то говорят о переносной симметрии.
Прямая АВ называется осью переноса, расстояние а элементарным переносом или
периодом.

а

АВ

симметрия животных

Симметрия в животном мире диктуется условиями жизни. Первые многоклеточные животные появились в воде.

Они произошли от колониальных простейших – жгутиковых, похожих на вольвокс, и располагались в толще воды во взвешенном состоянии. Любое направление для них было равноценно. Поэтому первые многоклеточные имели форму шара.

Такая форма идеальна для поддержания в наименьшем объёме наибольшего количества энергии. Они появились примерно 3,5 млрд. лет назад. Например, радиолярии. Животные, обладающие такой симметрией, существуют и в данное время, например, морские ежи.

Те животные, которые способны были передвигаться в каком-то избранном направлении, приобрели двустороннюю симметрию тела

На её появление важное влияние оказало как направление силы тяжести, так и направление движения животного в погоне за пищей или спасаясь от опасности. Для двустороннесимметричных видов характерно наличие двух примерно одинаковых частей тела, что помогает им сохранять равновесие, прямолинейно передвигаться, быстрее находить пищу и т

д. Билатерально симметричные организмы господствуют последние 650–800 млн. лет.

Это ракообразные, млекопитающие, птицы, насекомые. Билатеральная симметрия присуща большому количеству видов животных. Еж, сова, божья коровка, бабочка, рак, паук и другие животные обладают такой симметрией. Например, у бабочки симметрия проявляется с математической строгостью.

Ученые размещают виды симметрии животных (шаровую, радиальную, билатеральную) в эволюционный ряд.

Полностью асимметричная амёба считается более примитивным существом, чем одноклеточные организмы шаровой симметрии. Билатерально симметричные организмы считаются “венцом” эволюции.

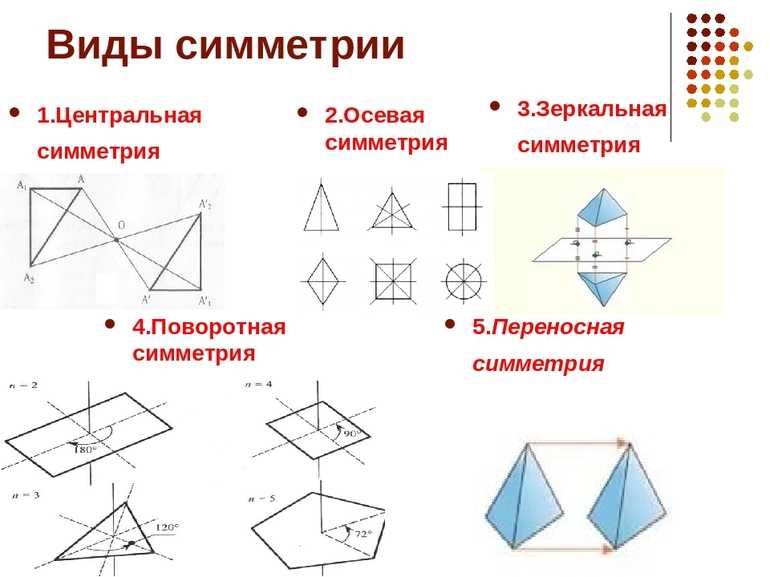
Определение понятия и виды

В Википедии о ней говорится как о фундаментальном природном принципе. В природе это явление может проявляться как в живых, так и в неживых формах. В неживой природе оно наиболее выражено в кристаллах. В растительном и животном мире — свойственно значительному числу организмов и проявляется в виде взаимного расположения одинаковых частей тела относительно его центральной оси.

Она не только обуславливает строение биологического тела, но и влияет на формирование определенных систем жизнедеятельности организма. Для многих живых форм наличие центральной оси тела отвечает за устойчивость в однородной среде и на поверхности, что объясняется, по-видимому, воздействием силы планетарного притяжения.

Эволюционное развитие жизни на планете Земля привело к возникновению такого вида существ, как Homo Sapiens — «Человек разумный», что предопределило появление социальной эволюции и таких закономерных понятий, как «культура», «цивилизация» и «социосистема».

На протяжении многих тысяч лет, в процессе наблюдения за природными объектами человеческими существами был сделан вывод о том, что наиболее жизнеспособными формами являются отвечающие основополагающему соответствию схожих частей друг другу относительно общего центра. Так родилось понимание принципа, который можно считать базовым для человеческой культуры как степени единства в организации жизнедеятельности людей.

В древнегреческом языке слово «симметрия» соответствовало понятию «соразмерность», образованному сочетанием слов «совместно» и «мерю»

Если рассматривать явление в архитектуре, то внимание следует уделить пропорциональному соотношению архитектурных деталей, их упорядоченности и красоте при взаимном расположении. Это формирует силуэт здания, воспринимаемый слева, справа, сверху и снизу, о чем в своем докладе, сделанном в Триеннале в 1951 г., упомянул выдающийся французский архитектор Ле Корбюзье.

Анализ выдающихся произведений зодчества позволяет выделить основные виды симметрии в архитектуре, используемые при создании строительных объектов:

• зеркальная;
• осевая;
• центральная;
• переносная;
• винтовая.